1. a)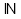 b) b)
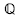 c)
c)
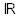 d)
d)
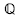 e)
e)
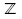 f)
f)
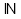 g)
g)
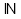
2. b) och d
3. a)
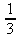 b)
b)
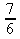 c)
c)
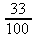 d)
d)
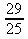 e)
e)
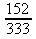 f)
f)
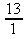
4. a)
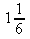 b)
b)
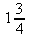 c)
c)
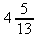 d)
d)
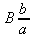 e)
e)
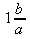 f) f)
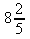 g)
g)
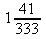
5. a) 0,12 b)
0,444... går inte att skriva som decimaltal c) 1,125 d) 103,0
e) 0,2648 f)
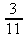 går inte att skriva som decimaltal g)
går inte att skriva som decimaltal g)
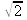 går inte att skriva i decimalform
går inte att skriva i decimalform
6. a)
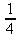 b)
b)
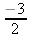 c) Talet 0 har inte ett inverterat tal för att
c) Talet 0 har inte ett inverterat tal för att
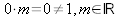 .
d) .
d)
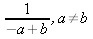 e) e)
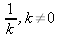 f) 1
f) 1
7. a)
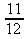 b) b)
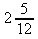 c)
c)
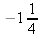 d)
d)
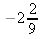
8. a)
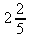 b)
b)
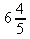 c)
c)
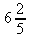 d)
d)
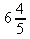 e)
e)
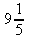 f)
f)
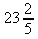
9. a) 0 b)
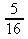 c)
c)
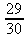 d)
d)
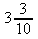 e) 1 f)
e) 1 f)
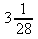
10. a)
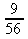 b)
b)
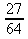 c) 0 d)
c) 0 d)
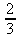 e)
0 e)
0
11. a)
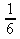 b)
b)
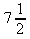 c)
c)
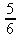 d) d)
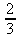
12. a)
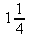 b)
b)
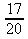 c)
c)
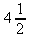 d)
d)
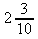
13. a) Ja b) Nej
c) Påstående:Roten
till ekvationen
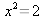 är inte ett rationellt tal.
är inte ett rationellt tal.
Motpåstående:
Ekvationen
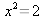 har
en rot av formen har
en rot av formen
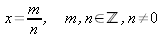 och där
och där
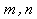 inte har några andra gemensamma faktorer än 1 eller -1.
Enligt motpåståendet gäller det nu att
inte har några andra gemensamma faktorer än 1 eller -1.
Enligt motpåståendet gäller det nu att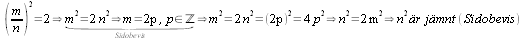
Så är
både m och n jämna och har den gemensamma faktorn 2. Denna
motstridighet visar att det ursprungliga påståendet
gäller.□
Sidobevis:
Påstående:A="x är ett jämnt heltal",
B="x2
är ett jämnt heltal",
 . .
Bevis:
i) Vi antar att x är jämnt
 x
är av formen x
är av formen
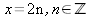 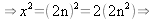 x2
är
jämnt. Alltså
x2
är
jämnt. Alltså
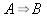 . .
ii)
Vi antar att x2
är jämnt och påstår att även x är
jämnt. Vi gör en antites: x är udda
 x
är av formen x
är av formen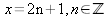
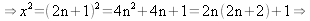 x2
är udda. x2
är udda.
Denna
motstridighet visar att påståendet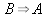 gäller. Av punkterna i) och ii) följer det att
gäller. Av punkterna i) och ii) följer det att
 □ □
|