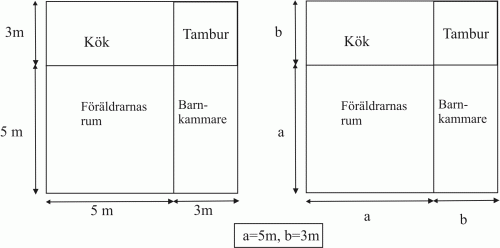
Kvadreringsreglerna

Kvadraten på en summa

Den finländska modellfamiljen med mamma, pappa och två barn äger ett kvadratformat hus. Här nedan i figur 4 har vi en planritning av huset.

Figur 4.

I vänstra delen av figur 4 ser vi att föräldrarnas rum är en kvadrat med sidan 5 m och tamburen en kvadrat med sidan 3 m. I högra delen av figur 5 har vi ersatt 5 m och 3 m med a respektive b.

Vi bestämmer arean av hela huset genom att först bestämma areorna av de enskilda rummen i vänstra delen av figuren:

På ett annat sätt är arean av hela huset i kvadratmeter .

Sedan bestämmer arean av hela huset genom att bestämma areorna av de enskilda rummen i högra delen av figuren. Nu änvänder vi bokstäver i stället för siffror.

På ett annat sätt är arean av hela huset . Härav följer nu att något som vi kan bevisa algebraiskt på följande sätt:. Vi har härlett minnesregeln för kvadraten på en summa.

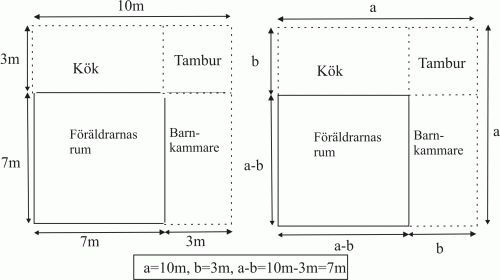
Kvadraten på en differens

Föräldrarna i en annan finländsk modellfamilj i grannskapet konstaterade att deras kvadratiska hus med sidan 10 m hade blivit för stort för att barnen hade flyttat ut till en annan ort. Pappan i familjen tänkte göra huset mindre men ändå behålla det kvadratiskt för att sänka värmekostnaderna. Här nedan i figur 5 har vi en planritning av huset. De streckade linjerna föreställer husets ursprungliga storlek. Pappan lämnade endast föräldrarummet kvar.

Figur 5.

I vänstra delen av figur 5 ser vi att föräldrarnas rum är en kvadrat med sidan 7 m och tamburen är en kvadrat med sidan 3m. Hela huset hade ursprungligen sidan 10 m. I högra delen av figur 5 har vi ersatt 10 m med a, 3 m med b och 7 m med a-b.

Vi bestämmer arean av huset i vänstra delen av figuren efter att pappan gjorde det mindre genom att först bestämma arean av föräldrarnas rum i kvadratmeter: .

På ett annat sätt är arean av föräldrarnas rum i kvadratmeter .

Sedan bestämmer vi arean av föräldrarnas rum genom att använda högra delen av figur 5 och bokstäver i stället för siffror. Föräldrarnas rum har arean för att det är en kvadrat med sidan .

Arean av föräldrarummet får vi också genom att först bestämma husets ursprungliga area. Den är . Av den här arean subtraherar vi areorna av tamburen , köket och barnkammaren . Så är arean av föräldrarummet . Härav följer nu att något som vi kan bevisa algebraiskt på följande sätt:. Vi har härlett minnesregeln för kvadraten på en differens.

Konjugatregeln

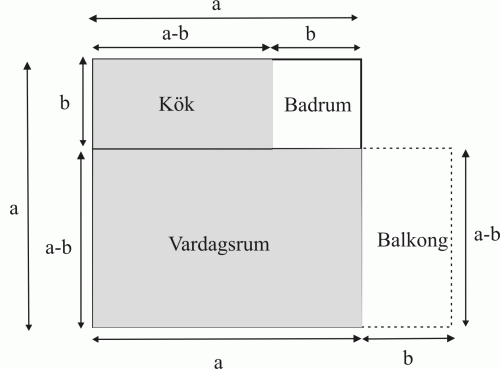
Med hjälp av konjugatregeln kan vi beräkna produkten av en summa och en differens.

Den utflyttade sonen i den finländska modellfamiljen bor i en studielägenhet. Planritningen av studielägenheten har vi i figur 6. Med hjälp av figuren bestämmer vi den sammanlagda arean av köket och vardagsrummet.

Figur 6.

Vi får den sammanlagda arean av köket och vardagsrummet genom att bestämma arean av den kvadrat som innehåller vardagsrummet, köket och badrummet. Sedan subtraherar vi av den här arean ytan av badrummet. Alltså .

Ett annat sätt att beräkna den sammanlagda arean av köket och vardagsrummet är att vi först märker att areorna av köket och balkongen är lika stora. Båda två har arean Så får vi den sammanlagda arean av köket och vardagsrummet genom att addera areorna av vardagsrummet och balkongen. Vardagsrummet och balkongen bildar tillsammans en rektangel med sidorna och . Alltså . Härav följer nu att något som vi kan bevisa algebraiskt på följande sätt:. Vi har härlett konjugatregeln.

Tilläpningar på minnesregler

Minnesreglerna, alltså kvadreringsreglerna och konjugatregeln, bör vi kunna utantill. Av det kommer vi att ha en stor nytta i fortsättningen. Dessutom gäller det att kunna tillämpa smidigt minnesreglerna åt båda riktningarna. Vi utvecklar uttrycket då vi skriver det som ett polynom utan parentes.

Exempel 1. Skriv som polynom med hjälp av minnesregeln för kvadraten på en summa.

Vi använder formeln. Nu är och. Så får vi .

Har du förstått? I

är lika med a)b) c)

Har du förstått? II

är lika med a) b) c)

Har du förstått? III

är lika med a)b) c)

Exempel 2. Skriv som polynom med hjälp av minnesregeln för kvadraten på en differens.

Vi använder formeln . Nu är och . Så får vi

Har du förstått? IV

är lika med a) b) c)

Exempel 3. Skriv som polynom med hjälp av konjugatregeln. a)

b) c)

Vi använder formeln i alla punkter.

I a)-punkten är och . Så är .

I b)-punkten är och . Vi får .

I c)-punkten är och .

Nu får vi .

Har du förstått? V

är lika med a) b) c)

Exempel 4. Skriv som polynom.

Enligt konjugatregeln får vi .

Har du förstått? VI

är lika med a) b) c)

Exempel 5. Skriv som polynom.

kan vi skriva på formen

Nu kan vi använda kvadreringsregeln. Vi får

Har du förstått? VII

är lika med a) b) c)

Har du förstått? VIII

är lika med a) b) c)

Har du förstått? IX

är lika med a)b) c)

Har du förstått? X

är lika med a)

b)

c)

Begreppsfrågor IV

1. Vad avses med minnesreglerna? Räkna upp dem vid namn.

2. Hur kan man geometriskt bevisa kvadreringsreglerna?

3. Med vilken regel kan man beräkna produkten av en summa och en differens?

4. Ett polynom består av kvadraten på en variabel, kvadraten på en konstant och dubbla produkten av variabeln och konstanten. Ge ett exempel på ett sådant här polynom. Kan man kvadrera polynomet?

5. Vilken regel skall man använda då man vill skriva en differens som en produkt?

6. Hur har man använt minnesreglerna i räkneoperationen?

Uppgifter

Skriv uttrycken i uppgifterna 1-4 som polynom. Förenkla uttrycken i uppgifterna 5-10.

1. a) b) c) d) e)
f)

2. a) b) c)
d)

3. a) b) c)

4. a) b) c)

5. a) b) c)

6. a) b)

7. a) b)
c)

8. a)
b)

9. a)
b)

10.*
Låt. Bestäm värdet avdå a) b).