|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PASS 8. EKVATIONSSYSTEM OCH EN LINJES EKVATION
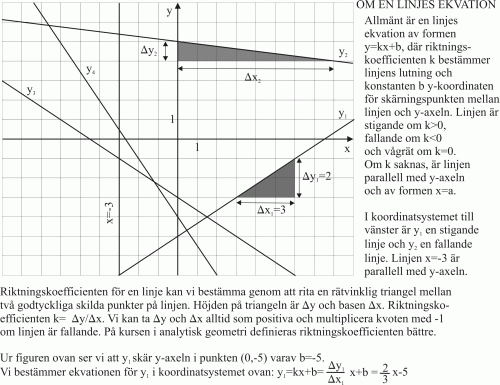
En linjes ekvation En linjes ekvation kan framställas i koordinatsystemet. Koordinatsystemet består av x-axeln och y-axeln. X-axeln är vågrät och y-axeln lodrät. Axlarna skär varandra i origo och står vinkelrätt mot varandra. Vi börjar med att behandla en linjes ekvation med hjälp av figur 7 och dess bildtext.
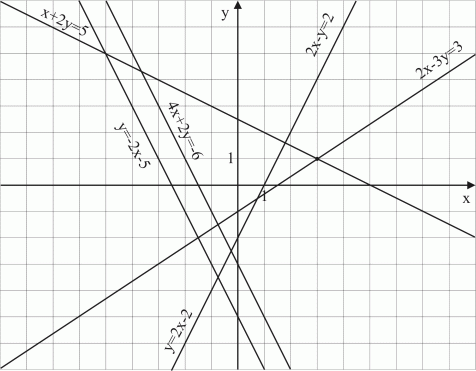
Grafisk lösning av ekvationssystem
Vår uppgift är att
grafiskt framställa ekvationerna
Alla punkter för vilka gäller att summan av x- och
y-koordinaterna är 2 ligger på linjen
Då
vi löser ut y ur ekvationen
Ekvationen
Ekvationen
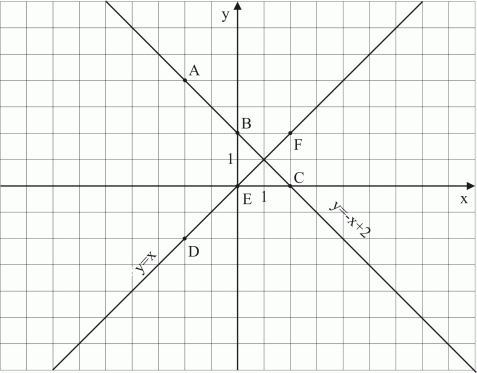
Nu placerar vi punkterna A, B, C, D, E och F ut i koordinatsystemet. Det har vi gjort i figur 8.
Vi ser ur figur 8 att linjerna
skär varandra i en enda punkt (1,1) som motsvaras av talparet
Exempel 1. Lös
grafiskt a)
Vi löser alla ekvationer med avseende på variabeln y och ritar ekvationernas motsvarande grafer i koordinatsystemet. Resultatet ser vi i figur 9.
a) Ur figur 9 ser vi att linjerna
2x-y=2 och y=2x-2 sammanfaller. Det är frågan om en och
samma linje. Oändligt många talpar satisfierar det givna
systemet. Systemet har lösningen
b) Vidare ser vi att linjerna
c) Ur figuren kan vi avläsa
att skärningspunkten är (3,1). Så har systemet
lösningen
Har du förstått? I
Systemet
Har du förstått? II
Systemet
a) är skilda parallella linjer b) sammanfaller c) har en gemensam punkt.
Har du förstått? III
Systemet
Algebraisk lösning av ekvationssystem Det är jobbigt att lösa ekvationssystem grafiskt. Ibland kan vi få en skärningpunkt som inte har heltalskoordinater och då är det definitivt frågan om en närmevärdeslösning. För att kunna lösa ekvationssystem exakt använder vi den algebraiska lösningsmetoden.
Additionsmetoden I additionsmetoden multiplicerar vi ekvationerna i systemet med sådana koefficienter att den ena eller den andra variabeln försvinner när vi adderar eller subtraherar ekvationerna ledvis. Vi får en summaekvation med en variabel. Vi löser den och får variabelns värde. Detta sätter vi in i någon av de ursprungliga ekvationerna. Genom att lösa den får vi värdet på den andra variabeln.
Exempel 2. Lös
systemet
Svar:
Insättningsmetoden I insättningsmetoden löser vi den ena ekvationen med avseende på den ena variabeln. Därefter sätter vi in uttrycket för den ena variabeln i den andra ekvationen. Vi får en ny ekvation med endast en variabel som vi kan lösa. Den andra variabeln får vi så att vi sätter in den ena variabeln i någon av de ursprungliga ekvationerna.
Exempel 3. Lös systemet
Vi löser ut y ur den övre
ekvationen:
Sedan insätter vi
Nu insätter vi
Har du förstått? IV
i)
Systemet
b) insättningsmetoden ii) Lös systemet.
Har du förstått? V
i)
Systemet
b) insättningsmetoden ii) Lös systemet.
Har du förstått? VI
Lös
systemet
a)
Begreppsfrågor VIII 1. Hur ritar man en linje i koordinatsystemet? 2. En linjes ekvation är grafiskt framställd i koordinatsystemet. Det vill säga att grafen till linjen har ritats i koordinatsystemet. Hur kan man avläsa linjens ekvation ur figuren? 3. Vad är ett ekvationssystem? 4: Förklara kort hur man löser ekvationssystem grafiskt. 5. Vilka dåliga sidor har den grafiska lösningsmetoden av ekvationssystem? 6. Konstruera och lös ett enkelt ekvationssystem som ansluter sig till det vardagliga livet. 7. Jämför additionsmetoden och insättningsmetoden vid algebraisk ekvationslösning.
Uppgifter
1. Rita linjerna a)
i koordinatsystemet.
2. Lös systemet a)
3. Lös systemet a)
4.Lös systemet a)
5. Använd figur 7 i den här uppgiften.
a) Bestäm ekvationen för
b) Bestäm det
ekvationssystem som fås av
Lös systemet och kontrollera resultatet grafiskt.
d) Bestäm ekvationerna för
6.
Lös systemet a)
7. Systemet
8. Undersök om linjerna a)
b)
c)
skär varandra i en och samma punkt. Tips: Det lönar sig att undersöka om två av linjerna skär varandra genom att bilda ett ekvationssystem och bestämma den möjliga skärningspunkten. Därefter ska man undersöka om den erhållna skärningspunkten satisfierar den tredje av ekvationerna.
9.* Lös systemet
Lös sedan ut x och y och därefter a och b.
Facit till Har du förstått-frågorna i pass 8 Facit till uppgifterna i pass 8  
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
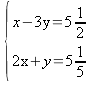 med
additionsmetoden.
med
additionsmetoden.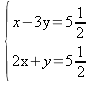 Vi
multiplicerar den nedre ekvationen med 3.
Vi
multiplicerar den nedre ekvationen med 3.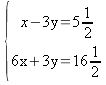 y
löser vi genom att insätta
y
löser vi genom att insätta


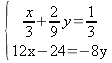
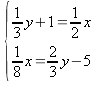
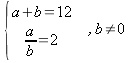
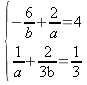 .
Tips det lönar sig att insätta
.
Tips det lönar sig att insätta