|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PASS 5. FAKTORISERING AV POLYNOM
Nyttan av faktorisering och faktorisering av heltal Har vi nytta av att kunna faktorisera polynom? Ja det har vi. Bra kunskaper i faktorisering av polynom möjliggör ett effektivt sätt att förkorta och förlänga uttryck. Dessutom kan vi med hjälp av faktorisering bestämma nollställen av olika uttryck och undersöka teckenväxling av uttryck. Vid lösning av ekvationer och olikheter är faktorisering en användbar metod. Goda kunskaper i faktorisering är till stor hjälp då vi studerar de första kurserna i lång matematik. En viktig förutsättning för att vi klarar oss bra i differentialkalkyl senare är att vi behärskar faktorisering utmärkt.
Enkelt sagt är faktorisering
multiplikation i motsatt riktning. Till exempel
är
Har du förstått? I De här talen är primtal a) 29,49 och 61 b) 97, 83 och 89 c) 0, 2 och 3.
Faktoriseringsmetoder för polynom Utbrytning av en gemensam konstant
Då vi faktoriserar ett
polynom skriver vi det som produkten av två eller flera polynom
vars grad är lägre än det ofaktoriserade polynomets
grad. Vid faktorisering av polynom skall vi alltid först
kontrollera om termerna i polynomet har en gemensam faktor som vi kan
bryta ut. Den hittar vi genom att studera variabeldelarna och
undersöka vad de har gemensamt. Vi bryter ut den största
möjliga gemensamma faktorn för termerna. Faktoriserar vi
Exempel 1. Faktorisera
polynomen a)
d)
a)
b)
c)
d)
e)
Alla punkter i exempel 1 kan vi
kontrollera genom multiplikation. Till exempel i c)-punkten får
vi
Har du förstått? II
Har du förstått? III
Minnesreglerna
I polynomet
Med hjälp av minnesregeln
för kvadraten på en summa kan vi faktorisera
Exempel 2. Faktorisera
polynomen a)
d)
a) Nu kan vi utnyttja regeln
b) Analogiskt med a)-fallet får
vi nu
c) 2, 10 och 50 har en gemensam
faktor 2. Vi kan bryta ut den. Så får vi
d) Nu har vi ett trinom. En av termerna är negativ. Den första och den sista
termen kan vi skriva som kvadrater och den mellersta termen och
dubbelt så stor som produkten av de termer som vi kvadrerade. I
det här fallet kan vi alltså använda minnesregeln för
kvadraten på en differens baklänges.
e) Nu är det helt klart att
båda termerna har en gemensam faktor
Har du förstått? IV
i)
ii)
iii)
Har du förstått? V
c)
Har du förstått? VI
b)
c)
Gruppering Användning av grupperingsmetoden förutsätter att vi har ett polynom med ett jämnt antal termer. Vi grupperar termerna så att varje grupp har samma faktor:
Exempel 3. Faktorisera a)
a)
b)
Har du förstått? VII
b)
c)
Exempel 4. Bestäm
konstanten
Då vi betraktar uttrycket
Har du förstått? VIII I faktorisering av polynom prövar man alltid först a) utbrytningsmetoden. b) konjugatregeln. c) kvadreringsreglerna.
Har du förstått? IX
i) b) kan faktoriseras med konjugatregeln. c) kan inte faktoriseras.
ii)
Faktorisera
Har du förstått? X
i) b) kan faktoriseras med kvadreringsregeln. c) kan faktoriseras med konjugatregeln.
ii)
Faktorisera
Begreppsfrågor V
1. Vad kallas multiplikation i motsatt riktning? Vilken nytta har man av det? 2. Hurdant tal är ett primtal? Ge exempel på primtal. 3. Räkna upp faktoriseringsmetoder för polynom. Klargör kort hur de fungerar. 4. Kan man använda grupperingsmetoden vid faktorisering om man har ett polynom med ett udda antal termer?
Uppgifter Faktorisera genom utbrytning i uppgifterna 1-5.
1. a)
2. a)
3. a)
4. a)
5. a)
d)
Faktorisera med konjugatregeln i uppgifterna 6 och 7.
6. a)
7. a)
f)
Faktorisera. Använd först utbrytning och sedan konjugatregeln i uppgifterna 8 och 9.
8. a)
9. a)
Använd kvadreringsregeln och faktorisera i uppgifterna 10-12.
10. a)
11. a)
12. a)
d)
Faktorisera med hjälp av gruppering i uppgifterna 13-17.
13. a)
14. a)
15. a)
16. a)
17. a)
Faktorisera först genom utbrytning och sedan vid behov med minnesreglerna eller gruppering i uppgifterna18-19.
18. a)
19. a)
c)
Faktorisera i uppgifterna 20-22.
20. a)
21. a)
22.* a)
23.* Bestäm det exakta
värdet av uttrycket
24.* Visa att summan av två udda tal är ett jämnt tal. Facit till Har du förstått-frågorna i pass 5 Facit till uppgifterna i pass 5  
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
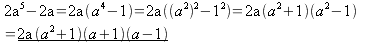
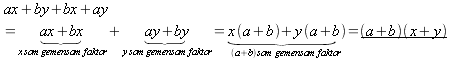
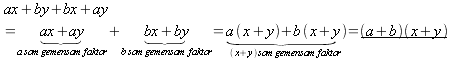
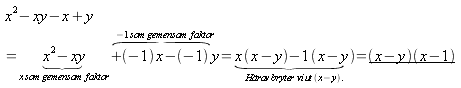
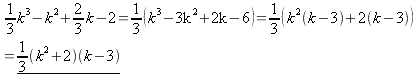 .
.