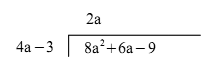|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PASS 3. POLYNOM, DIVISION AV POLYNOM MED UPPSTÄLLNING
Grundbegrepp om polynom
Ett polynom är ett uttryck
som kan skrivas som summan av ett antal termer. Ett polynom som
består av endast en term kallas monom, av två termer
binom och av tre termer trinom. Ett polynom kan inte innehålla någon variabel i
sin nämnare. Till exempel är
Exempel 1. Polynomet
grad har polynomet? c) Vilka koefficienter har termerna i polynomet? d) Ordna termerna i polynomet efter fallande grad.
Termerna är
Har du förstått? I
Polynomet
a)
Har du förstått? II
Polynomet
a) x och y b) x,y och a c) a.
Har du förstått? III
Polynomet
Räkneoperationer med polynom Sammanslagning av likformiga termer Termer med exakt samma bokstavsuttryck (variabeldel) kallas likformiga termer. Likformiga termer skiljer sig endast genom sifferkoefficienterna. Likformiga termer i ett polynom kan sammanslås något som vi gör då vi förenklar ett polynom. Vid sammanslagningen adderas koefficienterna. Variabeldelen förblir densamma.
Exempel 2. Låt
Har du förstått? IV
Polynomet
a)
Nollstället till ett polynom och beräkning av ett polynoms värde
Låt
Exempel 3. Bestäm
Har du förstått? V
Polynomet
Har du förstått? VI
Låt
Summan av polynom
Låt
Differensen av polynom
Låt
Produkten av polynom
Låt
=
=
= Vid bestämning av produkt använde vi termvis multiplikation och räkneregler för potenser. Därefter sammanslog vi likformiga termer.
Kvoten av polynom
Låt
Har du förstått? VII
i)
Differensen av polynomen
ii)
Summan av
polynomen
iii)
Produkten av polynomen
iv)
Kvoten av polynomen
Division av polynom med uppställning
Redan på skolans lägre
klasser har vi lärt oss att dividera
Exempel 4. Dividera med
uppställning
Vi ordnar först termerna i
täljaren enligt fallande grad. Så får vi
Den första termen
Sedan multiplicerar vi hela
nämnaren
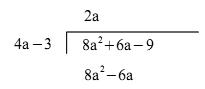
Därefter subtraherar vi
genom att byta alla förtecken i
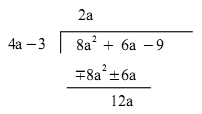
Differensen är 12a.
Sedan flyttar vi följande
term
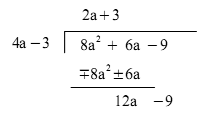
Nu är vi nästan färdiga. Vi utför bara multiplikation, teckenbyte och sammanslagning. 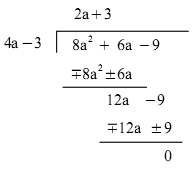
Vi märker att divisionen går
jämnt ut. Alltså
Vi kontrollerar vårt resultat med hjälp av multiplikationen
Exempel 5. Alla
polynomdivisioner går inte jämnt ut. Då vi
dividerar
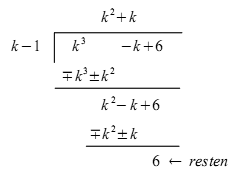
Alltså
Vi kan undvika polynomdivision med uppställning om divisorn i kvoten är ett monom. Ett polynom dividerar vi med ett monom termvis. Division med uppställning använder vi endast om divisorn är ett binom eller ett polynom med flera termer.
Exempel 6. Bestäm
kvoten
Har du förstått? VIII
Begreppsfrågor III 1. Vad är ett polynom för någonting? Ge exempel på polynom. 2. Hur skiljer sig monom, binom och trinom från varandra. Ge exempel på vartdera begreppet. 3. Hurdana termer är likformiga termer? Ge exempel på likformiga termer. 3. Vad kan man göra åt likformiga termer i ett polynom? 4. Vad avses med nollstället till ett polynom? Hur bestäms det? 5. Hur beräknas värdet av ett polynom? 6. Förklara allmänna principer vid division av polynom med uppställning. 7. I hurdana situationer kan polynomdivision med uppställning undvikas?
Uppgifter 1. Fyll i tabellen nedan.
2. Bestäm polynomets
3. Skriv termerna i polynomet
4. Ordna termerna i polynomet
5. Låt
6. Låt
7. Låt
8. Förenkla följande
uttryck a)
9. Bestäm
10. För vilket värde på
variabeln
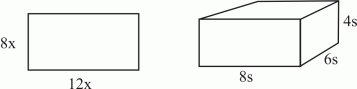
11. a) Beräkna omkretsen och arean av rektangeln i figur 3. b) Beräkna volymen av lådan i figur 3.
12. Låt
13. Låt
14. Utför divisionerna a)
15. Utför divisionerna med
uppställning. a)
16. Utför divisionerna med
uppställning.
a)
17.* Anta att
Facit till Har du förstått-frågorna i pass 3 Facit till uppgifterna i pass 3  
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
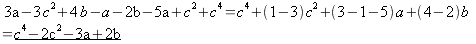
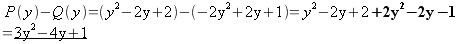 .
.