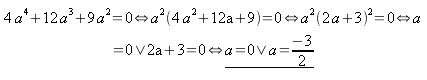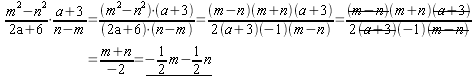Rationella uttryck

Kvoten av två polynom kallas ett rationelllt uttryck. Ordet rationell kommer av ett latinskt ord som betyder förnuftig. Det engelska ordet ratio betyder förhållande. Kvoten eller förhållandet av två polynom kallas alltså ett rationellt uttryck.

Exempel 1. Ge exempel på rationella uttryck.

Till exempel är och rationella uttryck. Även uttrycket är ett rationellt uttryck för att det kan skrivas på formen .

Rationella uttryck som inte är polynom kallas brutna rationella uttryck. Polynom däremot kallas hela rationella uttryck. Hos ett brutet rationellt uttryck finns det alltid en variabel i nämnaren.

Exempel 2. Ge exempel på hela och brutna rationella uttryck.

Till exempel är och brutna rationella uttryck. De har ju en variabel i nämnaren.

och är inte brutna rationella uttryck för att de inte har en variabel i nämnaren. Däremot är de hela rationella uttryck.

Allmänt har ett rationellt uttryck formen , där och är polynom och . är alltså inte definierat i nämnarens nollställen.

Har du förstått? I

är a) ett polynom b) ett helt rationellt uttryck c) ett rationellt uttryck.

Har du förstått? II

är a) ett brutet rationellt uttryck b) ett polynom c) ett helt rationellt uttryck.

Exempel 3. Låt Förbjud de värden på variabeln x för vilka inte är definierat det vill säga de värden på x för vilka inte går att bestämma. Bestäm .

Nu är nämnaren i uttrycket x-2. Vi måste förbjuda det x-värde för vilket x-2 antar värdet 0. Vi löser ekvationen Alltså x kan inte anta värdet 2, . Tecknet kallas ekvivalens. är ekvivalent med det att . Av det att följer att och tvärtom. I det praktiska livet är "det regnar" och "det är mulet" inte ekvivalenta med varandra. Det kan nämligen vara mulet fast det inte regnar. Däremot är "uppehållsväder" och "det regnar inte" ekvivalenta med varandra. Då vi bestämmer insätter vi i uttrycket . Vi får .

Har du förstått? III

Det förbjudna värdet för uttrycket är a) 2 b) 0 c) a.

Nollställen till rationella uttryck

Nollstället till det rationella uttrycket är det värde på x för vilket antar värdet 0. kan anta värdet 0 endast då täljarpolynomet. Nollställen för kan inte vara nollställen för . Det här kommer av definitionen för . är ju inte definierat då antar värdet 0.

Då vi multiplicerar med talet 0 är resultatet alltid 0:

,,och .

Enligt nollregeln för en produkt har produkten värdet 0 om och endast om minst en faktor i produkten har värdet 0:

I formeln ovan betyder tecknet ordet eller.

Exempel 4. Bestäm nollställen och förbjudna värden för a) b) c)

d) e) f)

a) är inte definierat då x=0. Uttrycket har nollstället .

b) är inte definierat då . Nämnaren har nollstället men det kan inte vara nollstället för uttrycket för att är ett förbjudet värde. Så saknar uttrycket nollställen.

c) är inte definierat då . Uttrycket har nollstället .

d) I pass 2 lärde vi oss att en potens med en jämn exponent har alltid ett positivt värde oberoende om basen är negativ eller positiv. En sådan här potens antar värdet 0 om och endast om basen är 0. Så kan vi säga att har för alla reella tal k ett värde större än eller lika med 0: . Den uppochnedvända A-bokstaven i formeln betyder "för alla". För att kan nämnaren i uttrycket endast få värden som är större än eller lika med 1. Nämnaren har således inte några nollställen. Det givna uttrycket saknar förbjudna värden. Det har nollstället .

e) har inte några förbjudna värden för att nämnaren alltid är 1. I pass 5 lärde vi oss att faktorisera polynom. faktoriserat är . Nollställena får vi med hjälp av nollregeln för en produkt .

f) har nämnaren 1 och således inga förbjudna värden. Nollställena för uttrycket bestämmer vi med hjälp av faktorisering och nollregeln för en produkt:

Har du förstått? IV

Uttrycket har nollstället a) 0 b) 1 c) .

Förenkling av rationella uttryck

I princip räknar man med rationella uttryck på samma sätt som med bråktal. Bråket kan vi skriva på formen och förkorta med 3: . Vi tar bråket och ersätter 3 med (x-1). Vi får . Här kan vi förkorta med x-1: .

Förkortning

Vi förkortar rationella uttryck så att vi först faktoriserar täljaren och nämnaren. Därefter förkortar vid med de faktorer som är gemensamma för täljaren och nämnaren.

Exempel 5. Förkorta följande uttryck a) b) c)

a)

b)

c)

Har du förstått? V

Då vi utför divisionen får vi a) b)

c)

Har du förstått? VI

Uttrycket förkortat är a) b)

c) Vi kan inte förkorta uttrycket.

Multiplikation

I pass 1 lärde vi oss att vid multiplikation av två bråktal multipliceras täljarna med varandra och nämnarna varandra och vid behov utförs förkortning. Precis på samma sätt gör vi med rationella uttryck. Innan vi multiplicerar faktoriserar vi och förkortar så mycket som möjligt.

Exempel 6. Utför multiplikationerna a) b) c)

a)

b) Vi ska inte multiplicera termvis utan det gäller för oss att faktorisera och förkorta.

c)

Har du förstått? VII

i) Vilket av följande ekvationskedjor är falskt?

a) b) c)

ii) Utför multiplikationen .

Division

Precis som med bråktalen multiplicerar vi med divisoruttryckets inverterade uttryck för att omvandla divisionen till multiplikation. Därefter fortsätter vi på samma sätt som med multiplikation.

Exempel 7. Utför divisionerna
a)

b)

c)

a)

b)

c)

I slutet har vi förkortat med . Svaret behöver vi inte förenkla vidare på formen .

Har du förstått? VIII

Utför divisionen

Addition och subtraktion

Att addera och subtrahera rationella uttryck utför vi enligt samma princip som addition och subtraktion av bråktal. Oliknämniga rationella uttryck måste vi först göra liknämniga genom förlängning. Uttryck med samma nämnare adderar/subtraherar vi så att vi adderar/subtraherar täljarna och åt summan/differensen ger vi samma nämnare.

Exempel 8. Förenkla följande uttryck
a)

b)

c)

d)

a)

b)

=

c)

=

d)

=

= Här var den minsta gemensamma nämnaren för uttrycken och . Detta fick vi genom att först faktorisera nämnarna i uttrycken och sedan välja ett möjligast enkelt uttryck som innehåller alla de olika nämnarfaktorerna.

Har du förstått? IX

är lika med

a)

b)

c)

Har du förstått? X

i) Då vi adderar måste vi förlänga det första uttrycket med x och det andra med y. Hur ska vi välja x och y? a) b) c)

ii)är lika med a) b) c)

Dimensionsanalys

Vad avses med dimension? En kropp har tre dimensioner; längd, bredd och höjd. Dimensionsanalys handlar ändå inte om en kropps utsträckning i rummet. Det är inte heller frågan om betraktelser med enbart meter, kvadratmeter och kubikmeter utan om betraktelser med alla möjliga enheter. Kort sagt är dimensionsanalys eller enhetsbetraktelse ett sätt att bli av med felaktiga formler.

Exempel 9. Kalle och Ville har en häftig diskussion. Diskussionen handlar om vem som har den rätta formeln för medelhastighet. Kalle påstår att formeln lyder och Ville håller fast vid formeln där v=medelhastighet, s=väglängd och t=tid. Båda pojkarna vet att hastigheten har enheten meter per sekund, m/s.

Pojkarnas lärare kontrollerar formlernas riktighet med dimensionsanalys. Med beteckningen avses att hastigheten har enheten meter per sekund. Med hjälp av dimensionsanalys och Villes formel uttrycker läraren . Det vill säga att enheten eller dimensionen för kvoten är eftersom tiden har enheten sekund och sträckan meter. Men nu blir enheten för medelhastigheten sekund per meter något som strider mot m/s. Således är Villes formel felaktig. Dimensionsanalys med Kalles formel ger och så har Kalle den rätta formeln.

Har du förstått? XI

Är storhetsekvationen felaktig då , , och ?

Räkneoperationer med storhetsvärden och enheter

Exempel på enheter är kilogram och meter. Pappan i den finländska modellfamiljen är 2 meter lång och väger 100 kilogram. 100 kg och 2 m är exempel på storhetsvärden. Ett storhetsvärde är produkt av ett tal och en enhet. I 100 kg är talet 100 och enheten kg.

Med storhetsvärden och enheter räknar man precis på samma sätt som vid förenkling av rationella uttryck. Man skall förhålla sig till uttryck med enheter som om de vore rationella uttryck.

Exempel 10. Kompisarna Kalle och Ville samt Kalles kusiner Linda och Tina köpte tillsammans 840 gram sötsaker. Med hjälp av en köksvåg delade de sötsakshögen i fyra mindre högar med samma vikt. Före delningen räknade var och en av dem vikten på sin kommande andel.

Kalle räknade så här:

Tina gjorde så här:

Lindas räknesätt finns här nedan:

Och Villes uträkningar såg ut så här:

Vilka av de här räknesätten är matematiskt korrekta? Kalles sätt är felaktigt för att där fattas enheten gram i högra ledet. Tinas sätt lider av ett liknande fel. Lindas och Villes sätt är exempel på rationella uttryck som har förenklats matematiskt korrekt. är inte samma sak som ! Men motsvarar matematiskt sett. I det praktiska livet finns det nog ingen människa som säger sig vara lång fast . Vid förenkling skall man ha enheterna hela tiden med eller lämna dem helt och hållet bort. Det förstnämnda rekommenderas med tanke på studier i fysik.

Exempel 11. Förenkla uttrycket med enheterna kilogram, meter och sekund.

Har du förstått? XII

Förenkla följande uttryck med enheterna kilogram, meter och sekund.

a) b) c) då och

Begreppsfrågor VI

1. Hurdant uttryck är ett rationellt uttryck?

2. Är alla rationella uttryck polynom?

3. Vad för en regel är nollregeln?

4. Varför måste man ta hänsyn till nämnarpolynomets nollställen hos rationella uttryck?

5. Berätta om multiplikation och division av rationella uttryck

6. Vilka likheter har addition och subtraktion av rationella uttryck med addition och subtraktion av bråktal?

Uppgifter

Förkorta uttrycken i uppgift 1.

1. a) b) c) d) e)
f)

Utför multiplikationerna och förkorta uttrycken i uppgifterna 2-4.

2. a) b) c)
d)

3. a) b) c)
d)

4. a) b)
c)

Utför divisionerna och förkorta uttrycken i uppgifterna 5-7.

5. a) b) c) d)

6. a) b) c)
d)

7. a) b) c)

Utför additionerna/subtraktionerna och förkorta i uppgifterna 8-12.

8. a) b) c)
d)

9. a) b) c) d) e)

10. a) b) c) d)

11. a) b) c)
d)

12. a) b)

Förenkla uttrycken i uppgifterna 13-14.

13. a) b)
c)

14.
a)

b)

15.* Bestäm värdet av uttrycket då och .