|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PASS 10. FUNKTIONER
Grundbegrepp om funktioner
Mamman i den finländska
modellfamiljen från pass fyra brukade dammsuga det 100 m2
stora huset varje lördag. Det tog 30 minuter. Efter att
pappan hade gjort huset mindre tog dammsugningen av det 49 m2
stora huset bara 14 minuter och 42 sekunder av mamman. I det 100 m2
stora huset offrade mamman
Har du förstått? I Avståndet från Helsingfors till Lahtis är 100 km. Om pappan i den finlänska modellfamiljen kör 100 km/h från Helsingfors till Lahtis är resetiden en timme. Om han däremot kör 120 km/h blir resetiden endast 50 min. Den tid som används åt resan Lahtis Helsingfors är beroende på a) avståndet Helsingfors-Lahtis b) hastighet c) ingetdera av a) och c).
Definition av en funktion En funktion är ett samband mellan två variabler där värdet av en variabel (beroende variabel, funktionsvärde) bestäms av värdet hos en oberoende variabel.
Då det gäller
dammsugning är variablerna städningstid och husets storlek.
Då vi gör så här måste vi anta att
städningshastigheten är en konstant. Städningstid är
en funktion av husets storlek. Det här sambandet kan vi beskriva
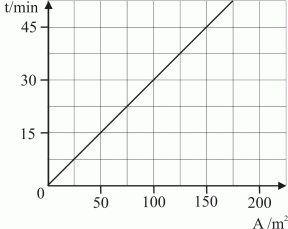
med hjälp av tabellen här nedan, med grafen i figur 15
eller med formeln
Linjen i figur 15 har ekvationen
Har du förstått? II
I
tabellen nedan har vi tre x-värden och motsvarande y-värden.
Tabellen beskriver funktionen
Funktionssambandet i tabellen kan beskrivas med formeln
a)
Beteckningar och begrepp med funktioner
Vanligen betecknas en funktion
med
Exempel 1. I ett funktionssamband ges varje naturligt tal x ett motsvarande naturligt tal y så att talet y är två gånger talet x. Bilda ett funktionsuttryck för det här sambandet.
Vi kan uttrycka det här sambandet på flera olika sätt:
a)
e)
Med en funktions definitionsmängd
(x-värdena)
Exempel 2. Låt
Vi
gör en tabell. Nu är -3, 0 och 3 de oberoende x-värdena.
De motsvarande av x beroende y värdena får
vi då vi insätter -3, 0 och 3 i stället för x i
funktionsuttrycket
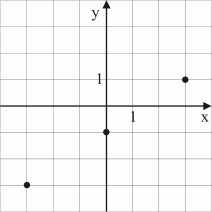
Grafen av den givna funktionen har vi i figur 16 här nedan.
Om definitionsmängden i
exempel 2 vore alla reella tal i stället för -3, 0 och 3
skulle grafen vara linjen
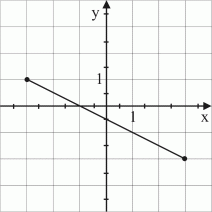
Har du förstått? III Här nedan i figur 17 ser vi grafen av en funktion f. 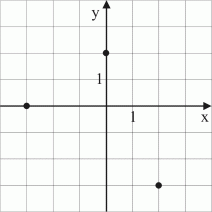 Figur 17.
I
figur 17 är
Har du förstått? IV
I
figur 17 är
En funktions nollställe är
det värde på den oberoende variabeln som ger
funktionsvärdet noll. Nollstället får vi genom att
lösa ekvationen
Exempel 3. Bestäm
nollstället till funktionen a) y då
a) Vi löser ekvationen f(x)=0.
b) Nu löser vi ekvationen
Svar: Nollstället är
Har du förstått? V
Funktionen
i figur 17 har nollstället a)
Exempel 4. I figur 18
nedan ser vi grafen av en funktion. Funktionen har definitionsmängden
a) Vi går från origo
till ettan på x-axeln och fortsätter nedåt. Då
b) Enligt figur 18 har den givna
funktionen en del av en linje som graf. Vi bestämmer linjens
ekvation enligt pass 8.1 och figur 7. Ur figur 18 ser vi att linjen
skär y-axeln i punkten
c)
d) Ur figur 18 ser vi att
y-värdena är mellan -2 och 2. Så har funktionen
värdemängden
e) Ur figur 18 får vi
grafiskt att
f)
Har du förstått? VI
Låt
Har du förstått? VII
Låt
Har du förstått? VIII
Nollstället
till funktionen
Begreppsfrågor X 1. Vad är en funktion?
2.
I ett funktionssamband ges varje naturligt tal
3. Förklara begreppen definitionsmängd och värdemängd. 4. Hur ritar man grafen till en funktion? Kan grafen till en funktion bestå av enstaka punkter? 5. Hur bestämmer man nollstället för en funktion? 6. Kan släktskapsförhållanden tolkas som funktioner?
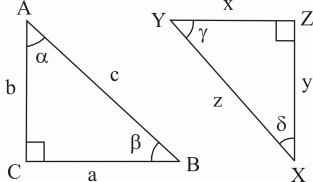
Uppgifter 1. Här nedan i figur 19 har vi två rätvinkliga trianglar.
Repetera definitionerna på
de trigonometriska funktionerna sinus, cosinus och tangens. Bestäm
med hjälp av figur 19. a)
e)
2. Firman Patriks Partaj hyr ut en festlokal. De debiterar en fast grundavgift på 100 euro och dessutom en avgift på 5 euro för varje gäst. Hur stor är festlokalshyran y om a) lokalen är uthyrd och inga gäster kommer b) lokalen är uthyrd och det kommer 10 gäster c) lokalen är uthyrd och det kommer x stycken gäster?
3. Låt
4. Bestäm nollstället
till funktionen a)
c)
5. Bestäm a)
6. I figur 20 nedan har vi grafen av en funktion. 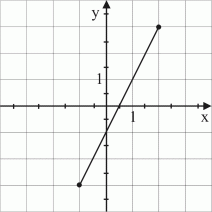 Figur 20.
Funktionen har värdemängden
b) Bestäm
d) Bestäm nollstället
till funktionen. e) För vilket värde på x är
7. Låt
8. Låt
9. En konstant funktion har samma
värde oberoende av variabelvärdet. Om
10.* Värdet av en funktion
kan ibland vara beroende av flere variabler än en variabel.
Ekvationen
11.* Exakt definierar vi funktionsbegreppet så här:
Det här symboliska språket kan översättas till svenska: En funktion från en mängd A till en mängd B är en regel som till varje element x i A entydigt ordnar ett och endast ett element i B.
Beskriver figur 21 en funktion a)
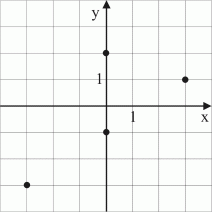 Figur 21.
12.* Använd den exakta definitionen för funktionbegreppet och besvara följande frågor: i) Ulrika har samtidigt två pojkvänner, Ulf och Hasse. Existerar det en funktion
ii) Ville sällskapar samtidigt med Linda och Lotta. Existerar det en funktion
Facit till Har du förstått-frågorna i pass 10 Facit till uppgifterna i pass 10  
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
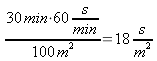 åt
dammsugning av en kvadratmeter. I det 49 m2 stora huset
krävde en kvadratmeter
åt
dammsugning av en kvadratmeter. I det 49 m2 stora huset
krävde en kvadratmeter
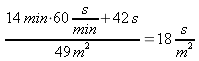 ,
alltså samma tid. Vi kan säga att den tid som mamman
behövde åt dammsugning var beroende av husets storlek.
,
alltså samma tid. Vi kan säga att den tid som mamman
behövde åt dammsugning var beroende av husets storlek.