|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PASS 7. EKVATIONSLÖSNING
Grundbegrepp om ekvationer En
ekvation säger att två matematiska uttryck är lika
stora. Ekvationen har alltså ett likhetstecken och två
deluttryck på var sin sida om likhetstecknet. Matematiska
påståenden, som har ett sanningsvärde, kallas
utsagor. Exempel på utsagor från pass 1 är
Exempel 1. Vilka av följande utsagor a) till f) är ekvationer ?
a)
b), d) och f) är ekvationer
för att de innehåller två deluttryck på var
sin sida om likhetstecknet. g) 4+5= är inte en ekvation för
att det inte finns någonting på höger sida av
likhetstecknet.
Har du förstått? I
Vilken
av följande utsagor är en ekvation? a)
Ekvationer kan man lätt lösa genom att tänka ut roten. En annan och bättre metod är att räkna ut roten.
Exempel 2. Lös
ekvationen
Vi kan tänka ut att roten är
Med "tänka ut"
-metoden fick vi svaret
Lösning av förstagradsekvationer
Vid förenkling av rationella
uttryck kunde vi förenkla dem endast så att värdet av
uttrycket inte förändrades. Till exempel kunde vi skriva
1. Vi kan addera samma uttryck eller samma tal till båda leden. Vi kan subtrahera samma uttryck eller samma tal från båda leden. Vi kan flytta termer över likhetstecknet till det andra ledet om vi samtidigt utför teckenbyte.
2. Vi kan multiplicera eller dividera båda leden med talet noll eller med ett uttryck som inte har värdet noll.
Exempel 3. Vi vet att
ekvationen
Exempel 4. Lös
ekvationen .
Vi kan kontrollera svaret så
att vi insätter
KONTROLL
Båda leden fick samma värde något som tyder på att vi har räknat ut roten rätt. Ekvivalenstecknet har vi använt i ekvationslösning och i kontrollen. I ekvationslösningen ovan är det inte obligatoriskt att använda ekvivalenstecknet. I fortsättningen lämnar vi bort det. Om man inte kan använda ekvivalenstecknet på rätt sätt är det bäst att lämna det helt och hållet bort. Så undviker man möjliga fel. I kontrollen ovan är det däremot obligatoriskt att använda ekvivalenstecknet för att vi har skrivit alla lösningsskeden på samma rad.
Har du förstått? II
i)
Lös ekvationen
ii)
Ekvationen
Exempel 5. a) Förenkla
det rationella uttrycket
b) Lös ekvationen
a)
b)
Har du förstått? III
I
ekvationen
med a) 6 b) 12 c) 3
Har du förstått? IV
Ekvationen
Exempel 6. I
gymnasiefysiken ingår bland annat termodynamik. I
termodynamiken finns formeln
Identiska ekvationer En ekvation, som satisfieras av alla eller inga variabelvärden, är en identisk ekvation. Vid lösning av identiska ekvationer försvinner variabeln. Om det sista lösningssteget är sant är alla reella tal lösningar. Om det sista lösningssteget är falskt saknar ekvationen lösning.
Exempel 7. Nu återkommer
vi till ekvationen
Svar:
Exempel 8. Lös
ekvationen
inte satisfieras av några reella tal.
Svar:
Har du förstått? V
Ekvationen
Har du förstått? VI
Ekvationen
Lösning av andragradsekvationer med hjälp av kvadratrötter Ekvationer, vars variabel är av andra graden, kallas andragradsekvationer. Vi lär oss att lösa andragradsekvationer med en speciell formel under senare gymnasiekurser. Nu fäster vi dock vår uppmärksamhet vid sådana andragradsekvationer som går att lösa utan formel.
Exempel 9. Lös
andragradsekvationen a)
a)
alltid minst 1. Det får aldrig värdet 0.
Svar:
Har du förstått? VII
Andragradsekvationen
Har du förstått? VIII
Begreppsfrågor VII 1. Vad är en ekvation för någonting? 2. Hur skiljer sig ekvationer från utsagor? 3. Berätta om sanningsvärden. 4. Förklara hur man löser förstagradsekvationer. Hurdana ledvisa operationer är tillåtna? 5. Nämn situationer i vardagslivet där man har nytta av ekvationslösning. 6. Förklara vad identiska ekvationer är. Ge möjligast enkla exempel på dem. 7. Skriv en vettig mening där begreppen kvadratrot, andragradsekvation och variabel förekommer.
Uppgifter Lös ekvationerna i uppgifterna 1-7.
1. a)
2.
a)
3. a)
4. a)
5. a)
6. a)
7. a)
Lös ekvationerna i uppgifterna 8 och 9 med avseende på variabeln x.
8. a)
9. a)
Lös andragradsekvationerna i uppgift 10.
10. a)
11. a) Lös r ur formeln
12.* I hållfasthetsläran
har total töjning
Facit till Har du förstått-frågorna i pass 7 Facit till uppgifterna i pass 7  
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
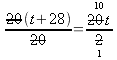 Vi
förkortar uttrycken i vänstra och högra ledet.
Vi
förkortar uttrycken i vänstra och högra ledet.