Grundbegrepp om olikheter

Vi får olikheter av ekvationer om vi byter ut likhetstecknet mot något av tecknen > (större än), ≥ (större än eller lika med), < (mindre än) eller ≤ (mindre än eller lika med). I en olikhet är två uttryck olika stora. I det praktiska livet har olikheterna en viktigare roll än ekvationerna. Pappan i den finländska modellfamiljen från pass 4 hade ursprunligen ett 100 m² stort hus. Innan han gjorde sitt hus mindre kände han intresse för hur stora hus de andra finländarna hade. Var han då intresserad av antalet andra familjer som hade precis ett lika stort hus som hans familj eller var han ute efter antalet familjer som hade ett större hus än 100 m²? Det senare, alltså olikheten, är en omständighet av väsentlig vikt i det här fallet.

Exempel 1. Vilka av följande utsagor a) till f) är olikheter ? Vilka av olikheterna har sanningsvärdet 1?

a) b) c) d) e) f) g)

a), c), e) och g) är olikheter. Av dem har c) och g) sanningsvärdet 1.

Då vi löser olikheter använder vi i stort sett samma regler som med ekvationer. 1. Vi kan addera samma uttryck eller samma tal till båda leden. Vi kan subtrahera samma uttryck eller samma tal från båda leden. Vi kan flytta termer över olikhetstecknet till det andra ledet om vi samtidigt utför teckenbyte. Vi kan multiplicera eller dividera båda leden med ett tal eller uttryck som är positivt. Om vi däremot multiplicerar eller dividerar båda leden med ett negativt tal eller uttryck måste vi byta riktningen på olikhetstecknet.

Exempel 2. När vi betraktar tallinjen i figur 10 är det helt klart att . Vi multiplicerar den här olikheten ledvis med . Så får vi talen och . Därimellan skriver vi tecknet > något som stämmer överens med tallinjetolkningen i figur 10. Alltså .

Figur 10.

Exempel 3. Lös olikheten .

Vi flyttar x till vänstra ledet och 6 till högra ledet och utför teckenbyte.

Vi förenklar båda leden.

Vi dividerar båda leden med -3. Olikhetstecknet byter riktning.

Svar: .

Har du förstått? I

Olikheten har lösningen a) b) c) .

Exempel 4. Lös olikheten .

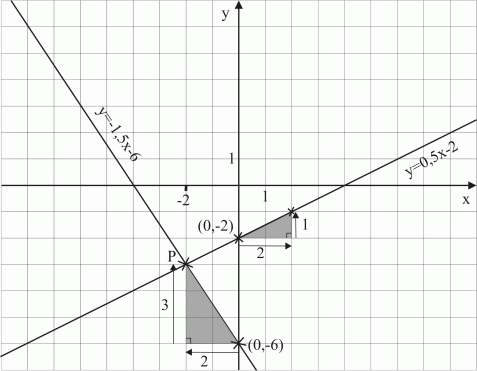
Vi kan lösa olikheten grafiskt genom att rita linjerna och i koordinatsystemet i figur 11. Linjen ritar vi så att vi först märker ut skärningspunkten mellan linjen och y-axeln. Den är (0,-2) enligt pass 8.1. Riktningskoefficienten är . Det vill säga att linjen är stigande. Den rätvinkliga triangel som vi ritar mellan punkten (0,-2) på linjen och den punkt som ligger till höger från (0,-2) har basen 2 och höjden 1. Till den här andra punkten kommer vi så att vi går från (0,-2) 2 steg åt höger och 1 steg uppåt. Vi förenar de här två punkterna och så har vi linjen .

Då det gäller linjen märker vi ut skärningpunkten mellan linjen och y-axeln, i det här fallet (0,-6). Riktningskoefficienten är nu . Linjen är således fallande. Den rätvinkliga triangel som vi ritar mellan punkten (0,-6) på linjen och den punkt som ligger till vänster från (0,-6) har basen 2 och höjden 3. Till den här andra punkten kommer vi så att vi går från (0,-6) 2 steg åt vänster och 3 steg uppåt. Vi förenar de här två punkterna och så har vi linjen .

Figur 11.

Vad betyder olikheten egentligen? Den frågar av oss för vilka värden på variabeln x linjen ligger ovanför linjen . Enligt figur 11 har linjerna skärningpunkten P=(-2,-3). Vi ser att till höger från den här punkten ligger ovanför . Olikheten satisfieras således av sådana x-variabelvärden som är större än x-koordinaten för P. Olikheten har således lösningen .

Vi kan också lösa olikheten algebraiskt, vilket ger ett exakt värde:

Vi flyttar till vänstra ledet och -2 till högra ledet och utför samtidigt teckenbyte.

Vi dividerar båda leden med 2 som är ett positivt tal.

Vi fick samma svar som med det grafiska lösningssättet.

Svar: Olikheten uppfylls då .

Har du förstått? II

I figur 12 nedan har vi ett koordinatsystem med linjerna och .

Figur 12.

I figur 12 satisfieras olikheten då a)b)c).

Har du förstått? III

I vilken punkt skär linjen y-axeln? a) (5,0) b) (0,5) c)

Har du förstått? IV

I figur 12 satisfieras olikheten då a) b) c) .

Har du förstått? V

I figur 12 satisfieras olikheten då a) b) c) .

Identisk olikhet

En olikhet, som satisfieras av alla eller inga variabelvärden, är en identisk olikhet. Vid lösning av identiska olikheter försvinner variabeln. Om det sista lösningssteget är sant är alla reella tal lösningar. Om det sista lösningssteget är falskt saknar ekvationen lösning.

Exempel 5. Lös olikheten a) b) c)

a) b) c)

en identiskt falsk

utsaga. en identiskt en identiskt

falsk utsaga sann utsaga (nu är

lika med alternativet med)

Svar: I a) och b) saknar olikheterna lösningar. I c) är alla reella tal lösningar.

Har du förstått? VI

Olikheten har a) inga lösningar b) lösningen c) lösningen .

Dubbelolikhet

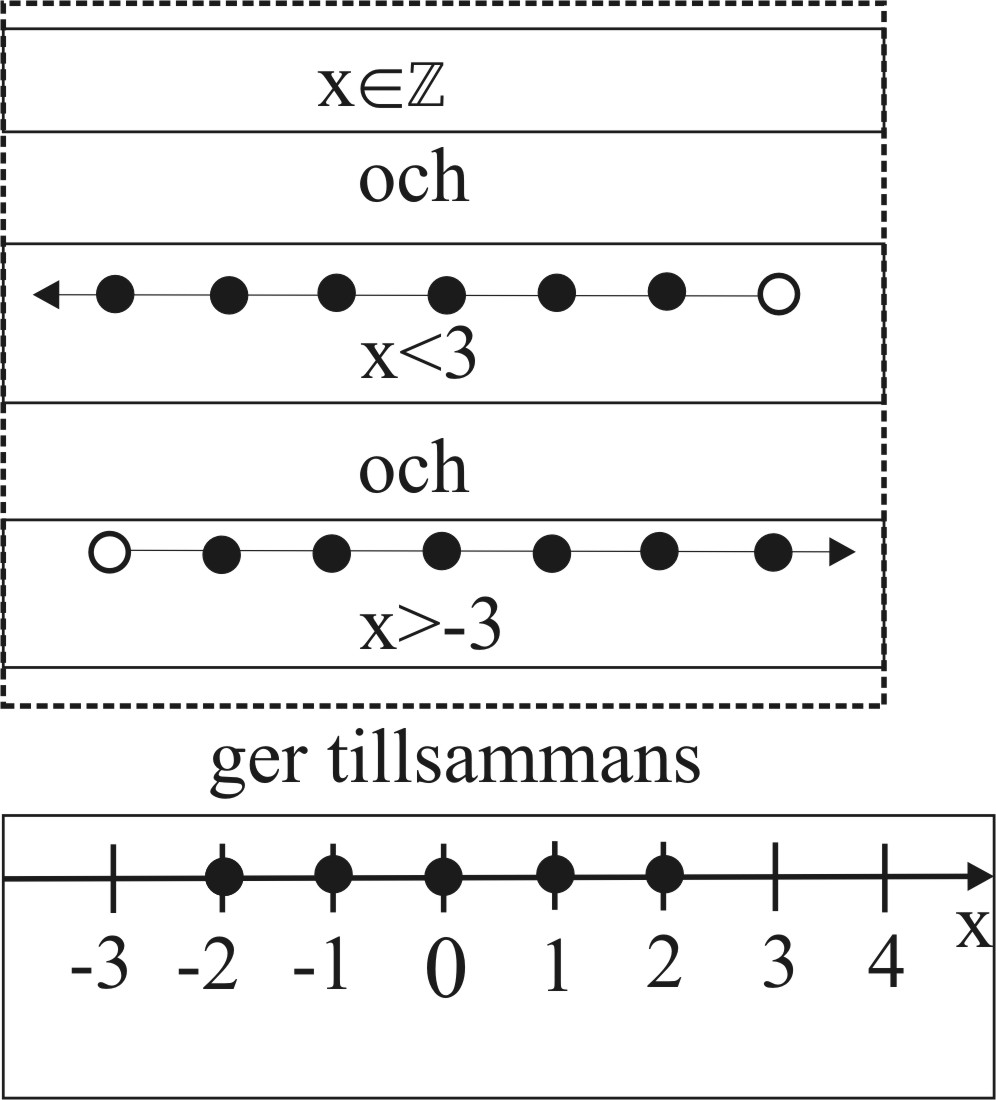
Vilka hela tal är större än talet -3 men mindre än talet 3? Villkoret i föregående frågan kan vi skriva på formen och . Villkoret kan vi skriva på formen . Således kan vi skriva villkoret och helt enkelt på formen . Ur figur 13 ser vi att sådana hela tal som ligger mellan -3 och 3 är -2, -1, 0, 1 och 2.

Figur 13.

Exempel 6. Skriv en möjligast enkel dubbelolikhet som har lösningen a) 1 b) 2 och 3 c) -3

a) b)

c) eller

Olikheter behandlar vi mera djupgående på de kommande kurserna i lång matematik. Då lär vi oss bland annat att lösa andragradsolikheter och olikheter av högre grad.

Har du förstått? VII

Antalet heltal som är större än -1 och mindre än 2 är a) 0 b) 1 c) 2.

Har du förstått? VIII

Villkoret ett heltal större än -1 och mindre en 2 kan skrivas som

a) dubbelolikhet b) två olikheter med ordet eller i mellan c) enkelolikhet

Begreppsfrågor IX

1. Beskriv vardagliga situationer då det är nödvändigt att använda olikheter.

2. Vad har lösning av olikheter gemensamt med lösning av ekvationer?

3. När byter olikhetstecknet i en olikhet riktning?

4. Hur kan man lösa olikheter grafiskt?

5. Förklara begreppen identisk olikhet och dubbelolikhet. Ge möjligast enkla exempel på vartdera begreppet.

6. Ekvationen är sann endast för värdet . Vad kan man konstatera om antalet sådana tal som uppfyller olikheten ?

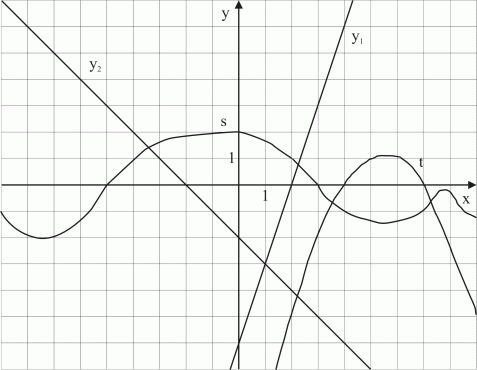
Uppgifter

I figur 14 nedan har vi ett koordinatsystem med ett antal linjer och kurvor.

Figur 14.

1. I figur 14 är kurvan t ovanför x-axeln då dubbelolikheten 4<x<7 gäller. Vilken dubbelolikhet gäller då kurvan s är ovanför x-axeln?

2. I figur 14 har vi linjerna och . Bestäm ekvationerna för linjerna. Lös algebraiskt olikheten . Kontrollera resultatet grafiskt med hjälp av figur 14.

3. Lös olikheten a) b) c) d) e)

4. Lös olikheten a) b) c) d)

5. Sätt rätt tecken ( >, ≥ , <, ≤ ) i den tomma rutan a) 67 b) -2 3 c) -8 -8 d) då är a 5 e) då är a 0 f) då är a 0 g) då är a 0

6. Lös den identiska olikheten .

7. Lös den identiska olikheten

8. Lös olikheten a) b) c)

9.* Hurdana värden kan konstanterna a,b och c anta då a) b) c)